Orbital elements
This section discusses orbital parameters. We focus on the implementation and conventions in REBOUND.
The following image illustrated the most important angles used. In REBOUND the reference direction is the positive x direction, the reference plane is the xy plane.
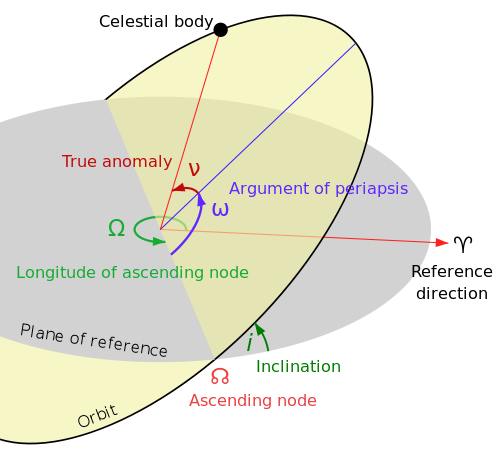
Orbit structure
| Variable name | Description |
|---|---|
d |
radial distance from reference |
v |
velocity relative to central object's velocity |
h |
specific angular momentum |
P |
orbital period (negative if hyperbolic) |
n |
mean motion (negative if hyperbolic) |
a |
semi-major axis |
e |
eccentricity |
inc |
inclination |
Omega |
longitude of ascending node |
omega |
argument of pericenter |
pomega |
longitude of pericenter |
f |
true anomaly |
M |
mean anomaly |
E |
Eccentric anomaly. Because this requires solving Kepler's equation it is only calculated when needed in python and never calculated in C. To get the eccentric anomaly in C, use the function double reb_M_to_E(double e, double M) |
l |
mean longitude = Omega + omega + M |
theta |
true longitude = Omega + omega + f |
T |
time of pericenter passage |
rhill |
Hill radius, \(r_{\rm hill} =a\sqrt[3]{\frac{m}{3M}}\) |
pal_h |
Cartesian component of the eccentricity, \(h = e\cdot \sin(pomega)\) |
pal_k |
Cartesian component of the eccentricity, \(k = e\cdot \cos(pomega)\) |
pal_ix |
Cartesian component of the inclination \(i_x = 2\cdot \sin(i/2)\cdot \cos(\Omega)\) |
pal_iy |
Cartesian component of the inclination \(i_y = 2\cdot \sin(i/2)\cdot \sin(\Omega)\) |
Important
All angles in REBOUND are in radians. Variables which have length, time or velocity units use code units.
Particle to orbit
The following function allows you to calculate the orbital elements of a particle.
struct reb_simulation* r = create_simulation();
reb_simulation_add_fmt(r, "m", 1.); // star
reb_simulation_add_fmt(r, "a e", 1., 0.1); // planet
struct reb_orbit o = reb_orbit_from_particle(r->G, r->particles[1], r->particles[0]);
printf("a=%f e=%f\n", o.a, o.e);
reb_orbit_from_particle function is the primary particle, i.e. the star or the center of mass.
sim = rebound.Simulation()
sim.add(m=1) # star
sim.add(a=1, e=0.1) # planet
o = sim.particles[1].orbit(primary=sim.particles[0])
print(o.a, o.e)
primary is not given, Jacobi coordinates are used.
You can also calculate the orbits of all particles in the simulation.
sim = rebound.Simulation()
sim.add(m=1) # star
sim.add(a=1, e=0.1) # planet
sim.add(a=2, e=0.1) # planet
orbits = sim.orbits()
for o in orbits:
print(o.a, o.e)
Conversion functions
True anomaly
The following function returns the true anomaly \(f\) for a given eccentricity \(e\) and mean anomaly \(M\):
double f = reb_M_to_f(0.1, 1.); // e=0.1, M=1.0
f = rebound.M_to_f(0.1, 1.0) # e=0.1, M=1.0
The following function returns the true anomaly \(f\) for a given eccentricity \(e\) and eccentric anomaly \(E\):
double f = reb_E_to_f(0.1, 1.); // e=0.1, E=1.0
f = rebound.E_to_f(0.1, 1.0) # e=0.1, E=1.0
Eccentric anomaly
The following function returns the eccentric anomaly \(E\) for a given eccentricity \(e\) and mean anomaly \(M\):
double f = reb_M_to_E(0.1, 1.); // e=0.1, M=1.0
f = rebound.M_to_E(0.1, 1.0) # e=0.1, M=1.0